In the section –I we have evaluated one spin system by using an one spin Hamiltonian act on a EigenFunction and then get the EigenValue, i.e. the Energy, For I=1/2, we obtain two Energy level, the transition between these two energy levels, we are able to calculate the Larmor Frequency. This is an observable parameter. Now we are using the same method to evaluate a two-spin system. It looks lots of writing, but it is still very simple. You need patient to look at them, and spend a little time to think why we write them in this way.
Before we start, I would like to clear some terms, that will make me easier to write:
υ=ω/2π υ (in Hz) ω (in rad S -1) ----- both of them descript frequency.
Ĥ one spin=-γB0Î z or Ĥ one spin= υ Î z ------ Hamiltonian of One spin along the Z component.
Ψ +1/2=Ψα and Ψ -1/2=Ψ β -------- EigenFunction of One spin (I=1/2)
For a two-spin system with no Coupling ---- they are not interacted each other.
Ĥ one spin= υ Î z then
Ĥ two spin = υ 1 Î 1z + υ 2 Î 2z They are not coupled
For a two-spin system with Coupling--- They are coupled with coupling constant J 12
Ĥ two spin= υ 1 Î 1z + υ 2 Î 2z + J 12 Î 1z Î 2z
Let’s work on the Hamiltonia of two-spin-system with no coupling first. υ 1 and υ 2 are the frequencies of the two spins respectively. Î 1z and Î 2z are the Operators of spin 1 and spin 2.
Their Eiganfunctions:
 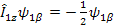
 
Now let’s calculate to show 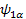 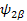 is an EigenFunction of the Hamiltonian: (υ 1 Î 1z + υ 2 Î 2z ), Also you may find is an EigenFunction of the Hamiltonian: (υ 1 Î 1z + υ 2 Î 2z ), Also you may find  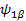 ; ;   ; ; 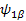 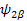 are also an EigenFunctions. are also an EigenFunctions.
Ĥ two spin 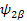 => (υ 1 Î 1z + υ 2 Î 2z ) => (υ 1 Î 1z + υ 2 Î 2z ) 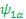 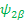
=> υ 1 Î 1z  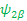 + υ 2 Î 2z + υ 2 Î 2z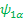 
=> υ 1 ( Î 1z 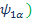 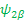 + υ 2 + υ 2 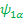 (Î 2z (Î 2z  ---- This is allowed because Î 2z operator has no effect on spin one function ---- This is allowed because Î 2z operator has no effect on spin one function 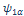 -- treat it as constant, we just swap the order. -- treat it as constant, we just swap the order.
=> υ 1(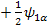 ) )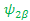 + υ 2 + υ 2 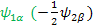
=> 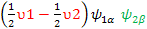 -- Here the EigenValue is -- Here the EigenValue is  and the EigenFunction is and the EigenFunction is 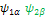
If we use other three EigenFunctions do the same thing as above, then the results as following:
  => =>  => E1 => E1
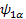  => + => + 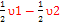 => E2 => E2
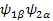 => => => E3 => E3
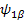  => => =>E4 =>E4
We assume 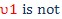 or equal to or equal to 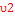 , then the Energy gaps: , then the Energy gaps:
E2-E1= - 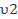 E3-E1= - E3-E1= -  or E4-E2= - or E4-E2= -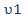 E4-E3= - E4-E3= - It simply shows two transitions, It simply shows two transitions,  and and  (or two frequencies contributed by two individual spins, they are not coupled. On the NMR spectrum, there are only two peaks that correspond to two frequencies. (or two frequencies contributed by two individual spins, they are not coupled. On the NMR spectrum, there are only two peaks that correspond to two frequencies.
Now if the two spins are scalar coupled ,the Hamiltonian will be:
Ĥ two spin= υ 1 Î 1z + υ 2 Î 2z + J 12 Î 1z Î 2z
The additional term J 12 Î 1z Î 2z , coupling term, describes the coupling of two spins. J is the coupling constant in Hz. The previous four Eigenfunctions ( , , 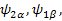  ) are still this new Hamiltonian’s EigenFunctions. But we will have a little different Eigen values. Let’s work on the first set of EigenFunction: ) are still this new Hamiltonian’s EigenFunctions. But we will have a little different Eigen values. Let’s work on the first set of EigenFunction: 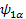 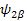 (The others are (The others are   , ,  , ,  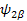 ). The calculations are the same: ). The calculations are the same:
Ĥ two spin 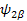 => (υ 1 Î 1z + υ 2 Î 2z + => (υ 1 Î 1z + υ 2 Î 2z + 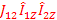 ) ) 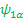 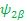
=> υ 1 Î 1z  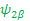 + + υ 2 Î 2z + + υ 2 Î 2z 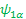 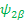 + +   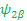
=> 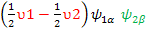 + +  ( ( ------- the first part is the same as above section. The second part, we can re-arrange them as show. Also we already have the result from above since J is a constant. ------- the first part is the same as above section. The second part, we can re-arrange them as show. Also we already have the result from above since J is a constant.
=> + +  ( ( ( ( ) )
=> 
=>(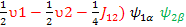
Now the new EigenValue is ( for the EigenFunction of for the EigenFunction of 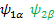 . If we calculate the other three Eigenfunctions, the results as following: . If we calculate the other three Eigenfunctions, the results as following:
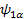  => =>  + + 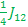 => E1 => E1
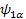  => + => +  - - 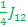 => E2 => E2
 => => - - 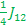 => E3 => E3
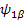  => =>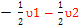 + + 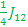 =>E4 =>E4
Then the Energy gap or transitions are:
E1 – E2 = 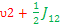
E3 - E4 = 
E1– E3 = 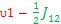
E2 – E4 =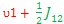
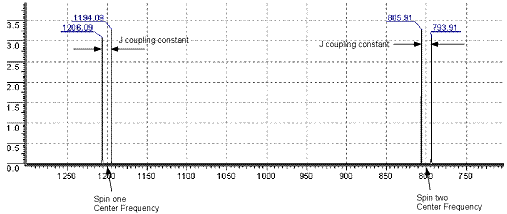
 The coupling constant is J Hz. So two coupled spins are placed in the magnet, there will be four possible of transitions which correspond to four frequencies. If two spins are protons, then they have the homonuclear coupling. See the figure above, two spins in the same spectrum. If two spins are different spins, such as 1H- 13C or 1H- 15N, then you will see one doublet in one spin spectrum, one doublet in the other spin’s spectrum. But they should have the same J coupling constant. The coupling constant is J Hz. So two coupled spins are placed in the magnet, there will be four possible of transitions which correspond to four frequencies. If two spins are protons, then they have the homonuclear coupling. See the figure above, two spins in the same spectrum. If two spins are different spins, such as 1H- 13C or 1H- 15N, then you will see one doublet in one spin spectrum, one doublet in the other spin’s spectrum. But they should have the same J coupling constant.
Before we continue, I would like to make the terms a little short and clean to see and write.
 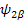 => αβ ------ the WaveFunction is not important as how they are written. Simplified to αβ. Also which one is 1 or 2 is not important, since basically they are same in this case. => αβ ------ the WaveFunction is not important as how they are written. Simplified to αβ. Also which one is 1 or 2 is not important, since basically they are same in this case.

For above example the transitions:
αα => αβ or αα => βα ------- Single Quantum Transition
αβ => ββ or βα => ββ ------- Single Quantum Transition
These are called single quantum transition, “allowed”. However,
αα => ββ ---- Double Quantum Transition --- “double flip”
αβ => βα ----- Zero Quantum Transition ------Double flip”
These two transitions are NOT Allowed, i.e. we cannot observe them directly. But we can indirectly detect these transitions by two-dimensional NMR (such as NOESY).
Before we go to the density Matrix theory, let’s look at a three coupled spin system. I will simply write the terms rather than repeated them as in two coupled spin system.
There are eight spin EigenFuctions.
ααα
ααβ αβα βαα
ββα βαβ αββ
βββ
The Hamiltonian:
Ĥ three spin= υ 1 Î 1z + υ 2 Î 2z + υ 3 Î 3z + J 12 Î 1z Î 2z + J 13 Î 1z Î 3z + J 23 Î 2z Î 3z
The Schrödinger Equation:
Ĥ three spin ααα= (υ 1 Î 1z + υ 2 Î 2z + υ 3 Î 3z + J 12 Î 1z Î 2z + J 13 Î 1z Î 3z + J 23 Î 2z Î 3z ) ααα
……. Total Eight of them by using different functions (ααα ααβ αβα βαα ββα βαβ αββ βββ).
After the calculation, we should have Eight EigenValues corresponding to eight functions.
ααα E1 =>  + +  + + 
αβα E2 =>  - - 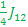 + + 
βαα E3 => 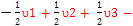 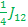 - - 
ββα E4=>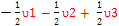 + +  - - 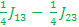
ααβ E5 =>  + + 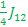 - - 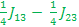
αββ E6=>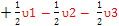 - - 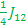 - - 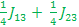
βαβ E7=> 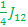 + + 
βββ E8=>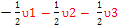 + + 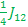 + + 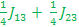
Let’s discuss these EigenValues in detail:
E3-E1=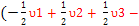 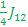 – –  ) – ( ) – (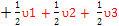 + +  + + 
E3-E1= -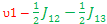 ; ;
E4-E2= -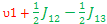 ; ;
E7-E5=-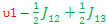 ; ;
E8-E6=-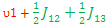 ; ;
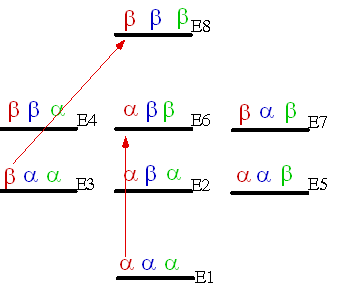
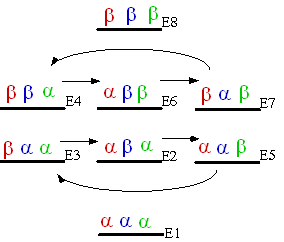
These four transitions are for spin one. The center frequency is  We can use an energy level diagram to show these transitions. Each energy level corresponding an EigenFunction, which is labeled as (ααα, αβα, etc.) the first letter is for the spin One, the second is for the spin Two etc. Since we use I=1/2 as a sample, they are only have two states, α or β. If I=1, then there are three states but the method is the same. We can use an energy level diagram to show these transitions. Each energy level corresponding an EigenFunction, which is labeled as (ααα, αβα, etc.) the first letter is for the spin One, the second is for the spin Two etc. Since we use I=1/2 as a sample, they are only have two states, α or β. If I=1, then there are three states but the method is the same.

The red is spin One, the allowed transition is E1 -> E3; E2 ->E4; E5 -> E6 and E6 ->E8. There are four transitions, and will have four NMR peaks corresponding to these transitions. For spin Two in Blue, there are also four lines, as well as spin three in Green. These transitions meet the transition rule +/- 1; we call it single quantum transitions. These transitions are easy to be observed by simple 1D NMR experiments. The NMR spectrum of each spin is a doublet-doublet.
I know you are going to get tired of these terms, but you only do once in your life time to understand what is going on here. Instead of reading, you can do them yourself.
On the other hand, the E1 -> E4, E1-> E6, E1 – E7, E3-> E8, E2->E8 and E5-> E8 (total six of them) are called double-quantum transition (+/- 2, two spins flip).
E4 – E1 =(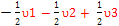 + +  - -  ) – ( ) – ( + + 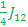 + + 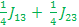 ) )
E4 – E1= -  - - - -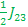
E8- E5 = -  + + + + 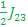 ----- Center frequency (- ----- Center frequency (- 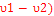
E7- E1 = -  - - - -
E8 –E2= -  + + + + 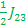 ------ Center frequency (- ------ Center frequency (- 
E6 – E1= -  - -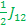 - -
E8 – E3= -  + +  + + 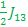 ------- Center frequency (- ------- Center frequency (- 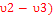
For the double quantum transition, it comes up three pairs of doublet. The center frequencies are the sum of two spins. For example, E1 -> E6 and E3 -> E8; the spin one (In Red), remain unchanged, by flip both spin two and spin three. The center frequency of the doublet is the sum of the Larmor frequencies of spin 2 and spin 3 with coupling J12 and J13.
Insert a spectrum here for the doublet to explain the center frequency plus their couplings.
There are six zero-quantum transitions.
E6-E4=( - - 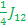 - - 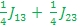 )-( )-( 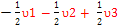 + + 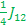 - - 
E6-E4 =  - -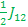 + + 
E5-E3= + +  - - 
E7-E6= 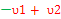  - -  or E6 – E7 = or E6 – E7 = 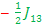 + +  ----Just change the sign. ----Just change the sign.
E3-E2=  - -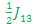 + + 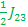 or E2 – E2 = or E2 – E2 = + +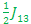 - - 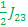
E7-E4=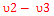 - - + + 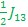
E5-E2=  + +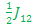 - - 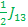
For Zero-Quantum transition, it comes up three pairs of doublet. The center frequencies are the difference of two spins. For example: E6 – E4, the spin two remain same, spin one and spin three flipped. The transition frequency is  - -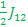 + +  ; the center frequency is ; the center frequency is  and one peak at ( and one peak at (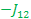 + +  . .
There are only one triple-quantum transition. All three states are flipped.
E8-E1= + + 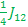 + + 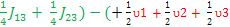 + +  + + 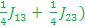
E8-E1=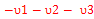 ------- The sum of the Larmor frequencies. A singlet!!! ------- The sum of the Larmor frequencies. A singlet!!!
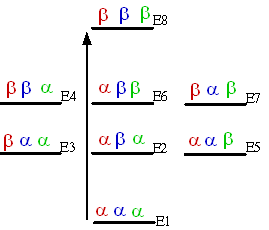
There are three more transitions: E5-E4, E3-E6 and E2-E7. All three spins are flipped. These lines are called combination lines. They can only be detected by multidimensional NMR. Also they are not connected with J coupling constant.

E5 –E4 =(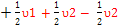 + + 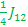 - -  + +  - - 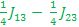 ) )
E5-E4 = 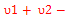 
E6-E3= 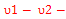 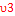
E7-E2=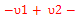 
After these calculations, we now understand how spins interact with the magnetic field and how the transition related to the frequency that we can observe it by NMR. Some transitions we cannot observe them in a simple NMR experiment, but we can design an experiment to observe them. So far we only discussed about the spins in the magnet field. Late on we are going to use our new tools (operators) to manipulate these spins in the magnet (doing NMR experiment) to observe their change in the magnet field.
Download PDF file
|