Now let’s get a work on something called Expectation Value.
From basic quantum theory, the value of an observable quantity A that could be represented by an operator  , can be found for any state i as the expectation value, <A> i. In other word, a value (size, how much, how big, how fast, where ?) of something (here is A), can be calculated by using its operator, i.e. the  act on a function or state function. For example:
 => If N=1 (one spin I=1/2, then k can be 1 and 2) then it is much clear to us: => If N=1 (one spin I=1/2, then k can be 1 and 2) then it is much clear to us: 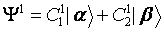 or as before. or as before.
More general term to use these functions for an Expectation Value :Z-component of angular momentum Iz:
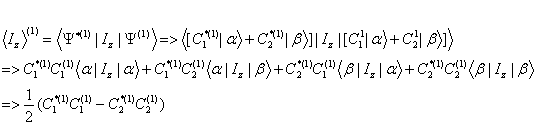
Omitted few steps from line two to line three, check previous section.
For Spin 2:
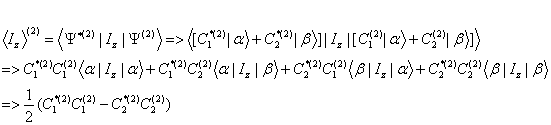
More general term to use these functions for an Expectation Value A:

Note: i, m and n are integers. The particular function of 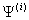 occur in an ensemble, the probability is P (i) occur in an ensemble, the probability is P (i)
If we can measure <A> many times, the probability:
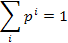
The overall expectation value will be :
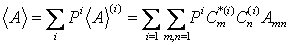
We want to know the value of A, we can calculate it from above equation. It tells us the average of value of many measurements, rather than the value of each measurement or a particular measurement. This value we called it --- Expectation Value --- In NMR we are more interested in 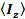 , ,  , ,  etc. etc.
The following few steps may be too fast, I will use a real sample to explain it in more detail.
From: 
Let 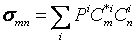 ------- Take the probability and coefficients of each measurement. ------- Take the probability and coefficients of each measurement.
Then:  --------- N is the spin number. One spin, N=1. --------- N is the spin number. One spin, N=1.

Tr means trace, we take the trace of matrix and add them together as the result------ Expectation Value A.
Where the σ is called the density operator, it has by definition a (2I+1) by (2I+1) dimensional matrix representation. For example, a spin I=1/2, the density operator has a two by two matrix. The average of observable is taking the trace of the product of A with σ. (Tr[σA) or Tr[Aσ].
Now let’s work on a real sample:
Note:
If one spin and I=1/2, the probabilities of occurrence, P 1 and P 2, are equilibrium, simply the populations of the states as determined by the Boltsmann distribution.

if we assume ε = ΔE/kT, and ε << 1. Thus, P 1 = ½(1+ ε/2) and P 2 = ½(1- ε/2). More correctly, the probability of spin stay in α state is P 1 = ½(1+ ε/2); and the probability of spin stay in β state is P 2 = ½(1- ε/2).
If we use above result:
 P 1 = ½(1+ ε/2) P 1 = ½(1+ ε/2)
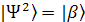 P 2 = ½(1- ε/2) P 2 = ½(1- ε/2)



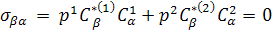
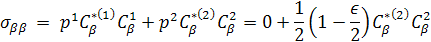
So σ can be written:
(the detail matrix representation will be discussed in the next section):
 or or
At equilibrium: 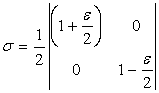 = =  è è
Were 1 is called the identity matrix or unit matrix of appropriate dimensions, here is 2x2 . It does not very with time and contributes to the measurement. The second term is important. At equilibrium, the density matrix can be written:
Note:
σ ασ =1/2[1 + (ε/2) + 0 σ αβ = 0 + 0
σ ββ = 0 + 1/2[1 - (ε/2) σ βα = 0 + 0
_______________________________________________________________________________________
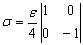
We can use this result to recalculate the Z-component of Angular momentum:
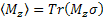
We want to use this density matrix (for I=1/2 and one spin) to calculate the magnetization of Z- component:
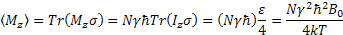
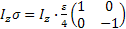 or or 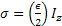
Where Mz = 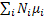 is the bulk magnetization that is the total of magnetic dipole moment μ . is the bulk magnetization that is the total of magnetic dipole moment μ .
The dipole moment 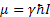 and and 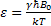 . (See any NMR book). . (See any NMR book).

Where 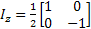 and and 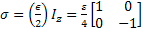
The Tr means add the diagonal number together. The final result is:

It tells us: The bulk magnetization of spin in the magnetic field B0 is directly proportional to N, the total number of spins in the system, and ϒ 2 magnetogyric ratio, the strength of the magnetic field.
*****************************************************************
Note:
Matrix Operation:
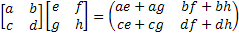
 = =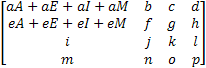
******************************************************************
Download PDF file
|