Let’s start a simplest case, ONE single spin (I=1/2). We have calculated the Energy level -> EigenValues, with its Hamiltonian Ĥ one spin=-γB0Î z with the EigenFunctions: Ψ +1/2=Ψα and Ψ -1/2=Ψ β . In previous discussion, we don’t have to know the Eigenfunction in detail. From the calculation, we are able to find its transitions and Larmor frequency when the spin in the magnet Bo.
The new idea is: we can construct a new WaveFunction by a linear combination of the EigenFunctions (we call the pure states such as Ψα Ψ β ). This WaveFunction is still an EigenFunction the Hamiltonian.
For Example:
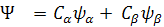 ----- a new function that is combination of the two EigenFunction. ----- a new function that is combination of the two EigenFunction.
Ĥ one spin Ψ= -γB0Î z (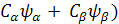
=> -γB0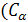 Î z Î z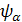 + +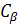 Î z Î z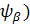
=> -γB0(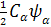 - (- - (-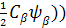
=>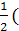 -γB0) ( -γB0) (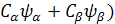
=>- γB0 Ψ -------- The EigenValue is still - γB0 Ψ -------- The EigenValue is still - γB0 and the EigenFunction is Ψ. The γB0 and the EigenFunction is Ψ. The 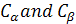 are just numbers, but importance of them are able to related to the time late on we will discuss it. The value ( are just numbers, but importance of them are able to related to the time late on we will discuss it. The value (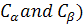 can be changed with time, or called time dependent coefficients. The WaveFunction (EigenFunction of the Hamitonian) is called superposition of states. Or a mixed state of a spin. can be changed with time, or called time dependent coefficients. The WaveFunction (EigenFunction of the Hamitonian) is called superposition of states. Or a mixed state of a spin.
If this is understandable, then we have following concept:
According to the principle of quantum mechanics, a spin system consisting of N nuclei, each of spin (if I = ½) there are 2 Nspin state functions i.e. φ1, φ2 for N=1, and φ1, φ2, φ3, and φ4 for N=2, etc. As well as there are 2 Nwavefunctions that describing the state of all nuclear spins, i.e. ψ 1, ψ 2 for N=1 and ψ 1, ψ 2, ψ 3 and ψ 4 for N = 2, etc. These wavefunctions can always be described as a linear combination of these spin state functions φ1, φ2 etc. That become a complete set of basis functions and it is specified by:
If I = ½ and only one spin, N=1, there will be two functions --- Eigenfunctions as a complete set:
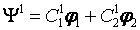 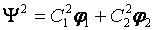
If I = ½ and two spins, N=2, there will be four functions --- Eigenfunctions as a complete set:
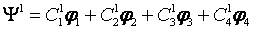 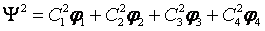
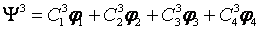 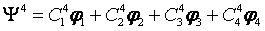
Or we can write a simple way:
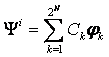 --------i =2 N k=1,2,3,4 ….. 2 N --------i =2 N k=1,2,3,4 ….. 2 N
Note: In previous section; we write them as 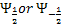 , Now we changed them a little. But they are same. , Now we changed them a little. But they are same.
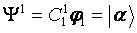 ; ß Ψ +1/2=Ψα if ; ß Ψ +1/2=Ψα if 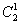 = 0 and = 0 and 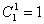
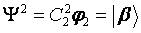 ; ß Ψ -1/2=Ψ β if ; ß Ψ -1/2=Ψ β if 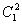 = 0 and = 0 and 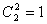
where φ k are spin EigenFunctions or the EigenStates of the Zeeman Hamiltonian. Since one spin and I= ½, there are only two possible energy levels, in convention, we write them as α and β state. We now could write them as:
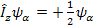 à à 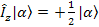
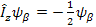 à à 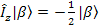
That is the same as we wrote before: 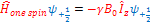 à à 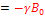 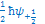 then then
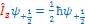 or or 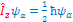 remove the remove the 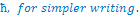
From now on, we use 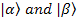 for I=1/2 spin. Before we continue, I would like to bring up two properties of these WaveFunctions: Just remember them, do not have to know why now. for I=1/2 spin. Before we continue, I would like to bring up two properties of these WaveFunctions: Just remember them, do not have to know why now.
Normalization: 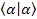 =1 or =1 or 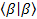 =1 in Math, we may write this way: =1 in Math, we may write this way: 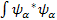 =1 =1
Orthogonality: 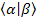 =0 or =0 or 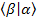 =0 =0
Now let’s use above sample to calculate it is normalized or not:
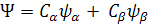 can be rewritten as can be rewritten as 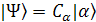 + + 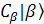 its complex conjugated function of its complex conjugated function of 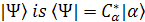 + +  , note the bra-ket has different direction. If we could approve , note the bra-ket has different direction. If we could approve 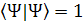 then they are normalized. then they are normalized.
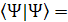 [ [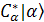 + + 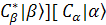 + + 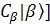
=>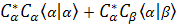 + +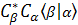 + +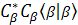
=>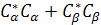 --- since the other two terms are zero [ --- since the other two terms are zero [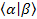 =0 or =0 or 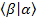 =0] . =0] .
The result is not zero!!! So the WaveFunction is not normalized. To normalize this function we have to dividing the function by:
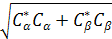 That is: That is:
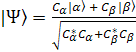 This will be a normalized WaveFunction if we do the calculation again as above. This will be a normalized WaveFunction if we do the calculation again as above.
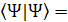 [ [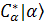 + + 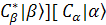 + + 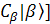 / /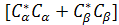 =1 =1
So these new WaveFunctions that are linear combined by original WaveFunctions can be normalized by multiple a constant.
####################################################################
Fact: In NMR calculation, the value of  are change with time (such as after RF pulse or during the RF pulse). But the value of [ are change with time (such as after RF pulse or during the RF pulse). But the value of [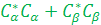 ] remains constant, no matter at what kind of pulses and directions. The value of ] remains constant, no matter at what kind of pulses and directions. The value of  only affect our scale of the result. So we just concede they were chosen to be equal ONE----- normalized. only affect our scale of the result. So we just concede they were chosen to be equal ONE----- normalized.
Download PDF file
|