In the last section, we got some kind of idea about the density matrix. It helps us to calculate the expectation value, ----- we are interested is the magnetization of a spin system. The simplest case is one spin with I=1/2. We use a 2x2 matrix. To represent a 2x2 matrix in terms of linearly independent matrix, we need 2 2 =4 ( for 4x4 matrix, we need 2 4= 16 of them). In NMR, we use 1, Iz Ix and Iy as a complete set of matrix operators. In fact, It is very easy to find them:
For example: the matrix representation of Iz is:
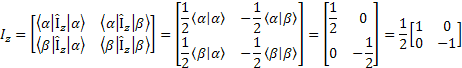
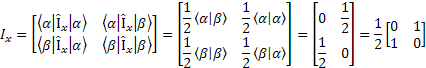
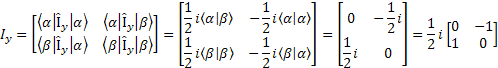
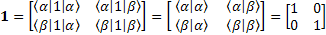
Note: This is the first time we mentioned Ix, Iy component of the angular momentum that is a Vector. At equilibrium they are zero. If we don’t send RF pulses to disturber the spin system, then we cannot observe the X and Y component of the angular momentum. We need these four operators to manipulate the spin system to get the specific information from the system.
The relationship between these operators is very important. First  and and  are the EigenFunctions of Iz, but not Ix and Iy, however, they have the following effects (Why? I don’t have chance to explain them yet. But keep them in mind now). are the EigenFunctions of Iz, but not Ix and Iy, however, they have the following effects (Why? I don’t have chance to explain them yet. But keep them in mind now).
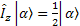 ; ; 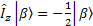 ; ;
 ; ; 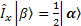 ; ;
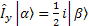 ; ; 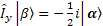 ; ;
 ; ; 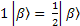
At Equilibrium:
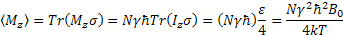
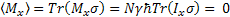
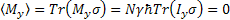
Where:
Tr Tr( Tr(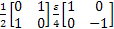 )=Tr( )=Tr(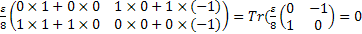
Tr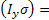 Tr( Tr( )=Tr( )=Tr(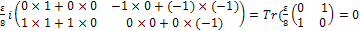
So at equilibrium, the magnetization of Mx and My are zero.
*************************************************
Here is a good time to expend our matrix to other spin systems. (So far we have worked out Matrices for one spin, I=1/2). For one spin (I=1/2), we just need four 2x2 matrices as a set of operators (1, Ix, Iy and Iz).
For one spin (I=1); i.e. we need (2I+1) 2=9 of 3x3 matrices as a set of operators. It can be Ix, Iy, Iz , Ix 2, ly 2,Iz 2,[Ix, Iz]+, [Ix,Iy]+, [Iy,Iz]+.
Ix=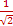 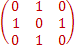
Iy=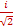 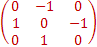
Iz=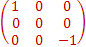
Ix 2=Ix • Ix=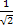 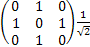 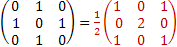
Iy 2=Iy • ly=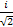 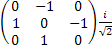 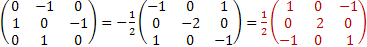
Iz 2=Iz •Iz=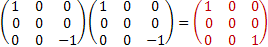
[Ix,Iz] +=IxIz +IzIx =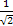 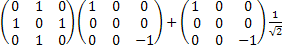 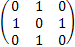
= + + = =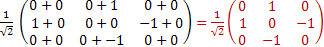
[Ix,Iy] +=IxIy+IyIx=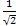 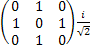 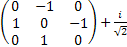 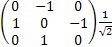 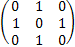
= + + = = = =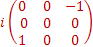
[Iy,Iz] +=IyIz+IzIy=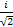 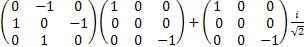 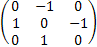
=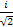 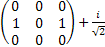 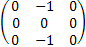 = =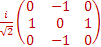
These matrixes in red are ready to use. As a matter of fact, we can make a table for them, just a chemical shift references. Download PDF file of Density Matrix representation.
Note:
i 2=-1
Matrix Operation:
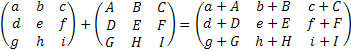
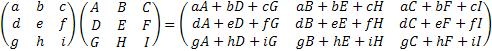
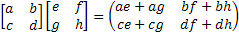
 = =
 Ix= Ix= = =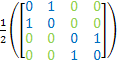
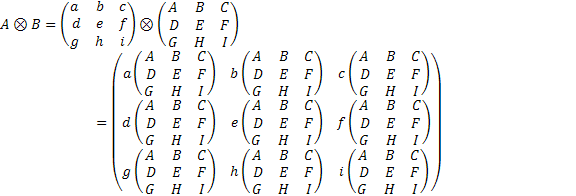
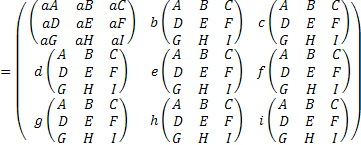
=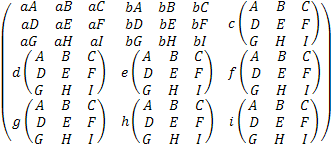
Download PDF file
|
|